Cordones y Coordenadas

El Ecuador continental¹ posee una extensión un poco mayor a 246 mil km². Es sencillo verificar este dato, si uno cuenta con la cartografía oficial; en esta tarea, sf::st_area() es la función clave:

library(sf)
library(units)

Ecuador_sf = read_sf("boundaryl.shp")$geometry %>% # fuente: http://www.igm.gob.ec/
   st_cast("POLYGON") %>% st_set_crs(32717) # proyección oficial: UTM zona 17S

st_area(Ecuador_sf) %>% set_units("km^2") %>% format(digits = 8)

## [1] "246039.89 [km^2]"

Resulta trivial calcular cantidades como áreas o distancias, pero aprender la lógica detrás de tales operaciones nunca dejará de resultar interesante. En este artículo revisaremos un acercamiento al problema de calcular el área de un polígono: la shoelace formula². Este curioso nombre, como se verá, proviene de la forma como se construye la fórmula.

Plantear dicho problema supone conocer las coordenadas \(P_i = x_i,\ y_i;\ i = 1, 2, ... n\) de los vértices del polígono, donde \(n\) es el número de vértices (y también es el número de lados). Es un requisito que estos vértices se encuentren ordenados alrededor del límite; dicho de otra manera, que el polígono se trace “uniendo los puntos” en orden. Tomemos el siguiente gráfico; en este ejemplo, el área del triángulo \(A = \triangle P_1 P_2 P_3\) será la interrogante.

El rectángulo \(E = A + B + C + D\) se traza de manera que contenga al triángulo \(A\), su área sea mínima, y sus lados sean paralelos a los ejes. En este caso³ es sencillo calcular el área de \(E\) y de los triángulos \(B, C, D\) con fórmulas geométricas elementales: \(bh\) y \(\frac{1}{2} bh\) respectivamente.

\[E = (x_2 - x_3) (y_3 - y_1)\] \[D = \frac{1}{2} (x_1 - x_3) (y_3 - y_1)\] \[C = \frac{1}{2} (x_2 - x_3) (y_3 - y_2)\] \[B = \frac{1}{2} (x_2 - x_1) (y_2 - y_1)\]

Ahora, es evidente que el área buscada se puede hallar por diferencia: \(A = E - B - C - D\). Reemplazando y simplificando se obtiene:

\[ \begin{equation} A = \frac{1}{2} (x_1 y_2 - x_2 y_1 + x_2 y_3 - x_3 y_2 + x_3 y_1 - x_1 y_3) \tag{1} \end{equation} \]

En este ejemplo:

\[ \begin{equation} A = \frac{1}{2} (8\cdot6 - 9\cdot2 + 9\cdot7 - 1\cdot6 + 1\cdot2 - 8\cdot7) = 16.5 \end{equation} \]

De manera que el problema está resuelto, al menos cuando el polígono es un triángulo. Con todo, revisemos que sucede si variamos este ejemplo, intercambiando las posiciones de \(P_2\) y \(P_3\).

Según la ecuación (1):

\[ \begin{equation} A = \frac{1}{2} (8\cdot7 - 1\cdot2 + 1\cdot6 - 9\cdot7 + 9\cdot2 - 8\cdot6) = -16.5 \end{equation} \]

Es un resultado importante pues, mientras el valor absoluto del área sigue siendo correcto, el hecho de que haya cambiado de signo resultará crucial más tarde. La regla es la siguiente: si los vértices se encuentran ordenados en sentido antihorario, se calcula un área positiva; si el orden es horario, se calcula un área negativa.

Revisemos una variación más, reemplazando \(P_3\) por \(P_0 = 0,\ 0\).

Cuando uno de los vértices es el origen, es posible reducir (1):

\[ \begin{equation} A = \frac{1}{2} (x_1 y_2 - x_2 y_1 + x_2 \cdot0 - 0\cdot y_2 + 0\cdot y_1 - x_1\cdot0) = \frac{1}{2} (x_{1}y_{2} - x_{2}y_{1}) \tag{2} \end{equation} \]

En este ejemplo:

\[ \begin{equation} A = \frac{1}{2} (8\cdot7 - 1\cdot2) = 27 \end{equation} \]

Ahora podemos verificar que se calcula un área positiva, pues los vértices se encuentran en sentido antihorario. La ecuación (2) puede ser generalizada a:

\[ \begin{equation} \triangle P_0 P_i P_{i+1} = \frac{1}{2} (x_i y_{i+1} - x_{i+1} y_i);\ i = 1, 2, ... n \end{equation} \]

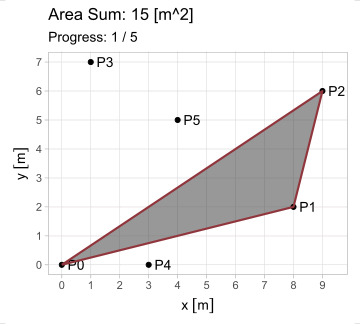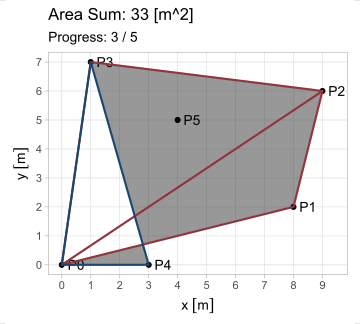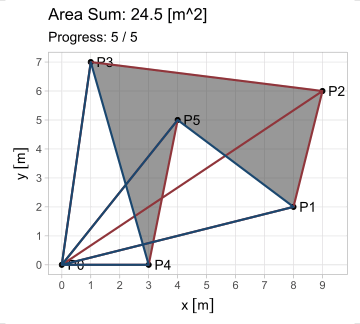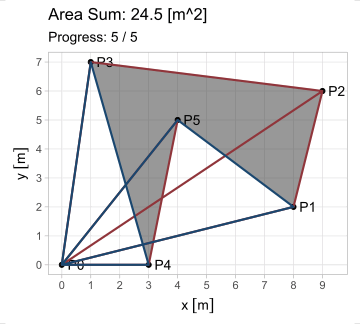
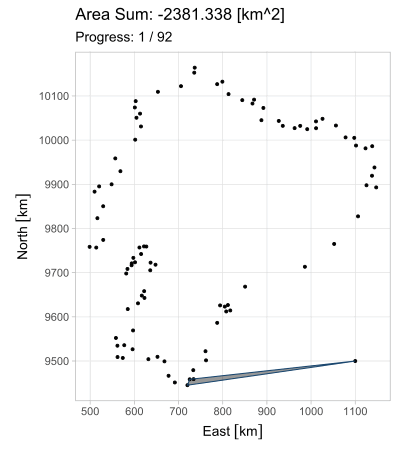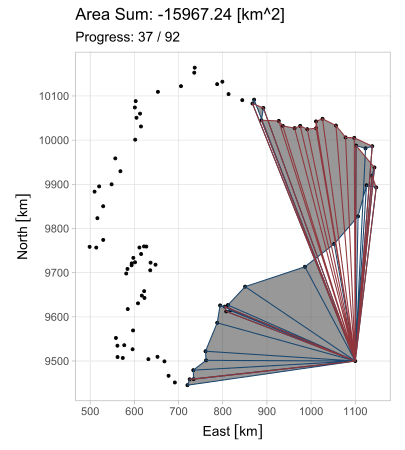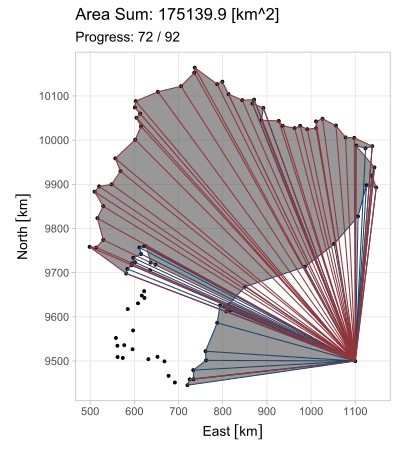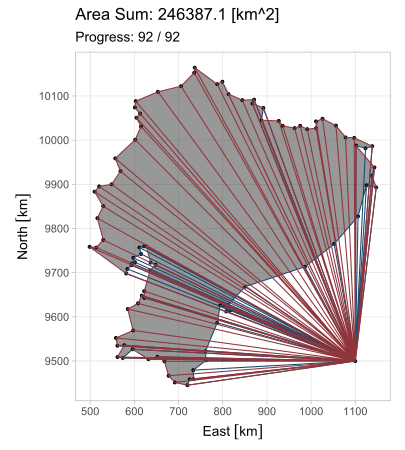
Esta forma es aplicable en cada uno de los \(n\) lados, observando que el vértice \(P_{n+1}\) equivale a \(P_1\) (pues el polígono se encuentra cerrado). Pero ¿cuál es el propósito de generalizar esta ecuación? Observen lo que sucede al iterarla en el triángulo \(A\) del primer ejemplo; en estas animaciones, los triángulos de borde rojo poseen área positiva; los de borde azul, negativa.

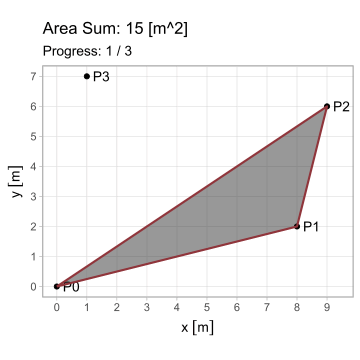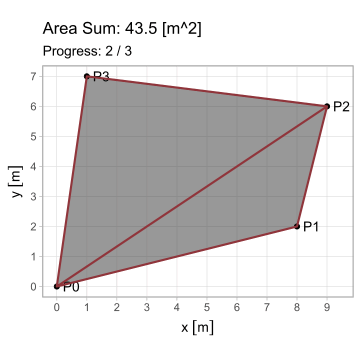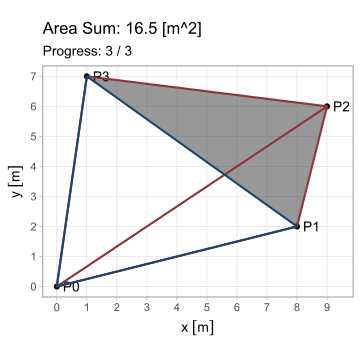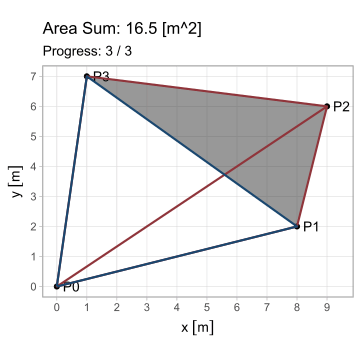
El hecho de que esta fórmula devuelva resultados positivos y negativos resuelve el problema del área para cualquier polígono \(P_1 P_2 ... P_n\); calculándola en todos los lados, se generan triángulos cuyas áreas, sumadas, producen el polígono buscado. Existe, sin embargo, la restricción de que el polígono sea simple (no se debe intersecar a sí mismo).

\[ \begin{equation} A_{P_1 P_2 ... P_n} = \triangle P_0 P_1 P_2 + \triangle P_0 P_2 P_3 +\ ...\ \triangle P_0 P_n P_1 \end{equation} \]

\[ \begin{equation} A_{P_1 P_2 ... P_n} = \sum_{i=1}^n \triangle P_0 P_i P_{i+1} = \frac{1}{2} \sum_{i=1}^n (x_i y_{i+1} - x_{i+1} y_i);\ P_{n+1} = P_1 \tag{3} \end{equation} \]

Y esta es la shoelace formula. Su construcción, multiplicando de manera cruzada las coordenadas de un vértice con el siguiente, se asemeja a insertar los cordones en un zapato. Compliquemos un poco nuestro ejemplo, añadiendo dos vértices:

Otro nombre que se le ha otorgado es surveyor’s formula pues su utilidad en topografía salta a la vista; en esta aplicación, un paso previo era transformar las coordenadas polares, del teodolito, a rectangulares. \(P_{0}\) representaría la ubicación del topógrafo, y este punto no tiene que ser el origen necesariamente; reutilizando (1) es posible desplazarlo a cualquier ubicación.

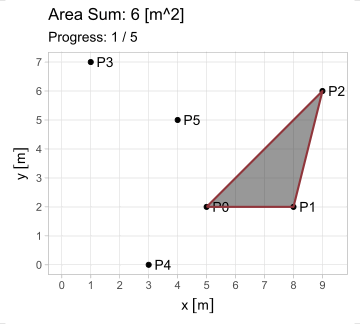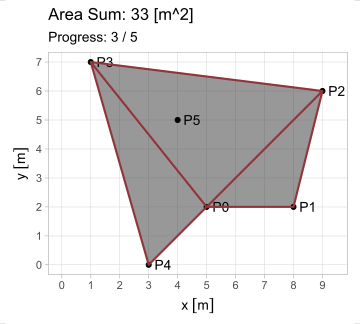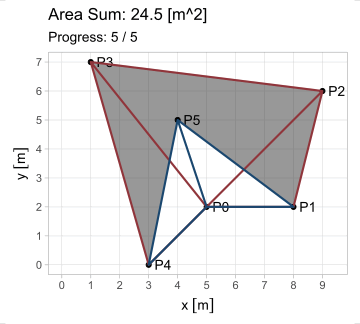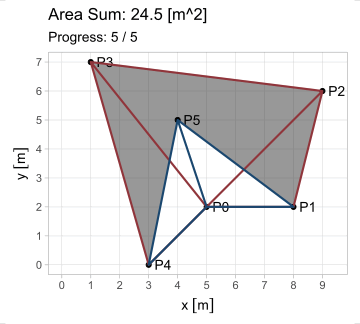
La fórmula encuentra una aplicación más en el cálculo del centroide, el cual es el centro de masa del polígono. Si \(A\) es el área calculada con la shoelace formula (incluyendo su signo positivo o negativo), las coordenadas del centroide \(P_c = x_c,\ y_c\) se hallan con el siguiente par de fórmulas:

\[ \begin{equation} x_c = \frac{1}{6A} \sum_{i=1}^n (x_i + x_{i+1}) (x_i y_{i+1} - x_{i+1} y_i) \tag{4} \end{equation} \]

\[ \begin{equation} y_c = \frac{1}{6A} \sum_{i=1}^n (y_i + y_{i+1}) (x_i y_{i+1} - x_{i+1} y_i) \tag{5} \end{equation} \]

Nuevamente, calcular el centroide de un polígono es algo trivial; en el caso del Ecuador continental, por ejemplo, podemos ejecutar sf::st_centroid(Ecuador_sf), obteniendo como resultado:

## POINT (793562.37 9841009.5)

Con todo, ahora estamos en capacidad de replicar esas funciones sf. El primer paso es transformar los datos espaciales en una matriz de coordenadas.

Ecuador_df = st_cast(Ecuador_sf, "POINT")[-1] %>%
   lapply(as.double) %>%
   Reduce(rbind, .) %>%
   set_units("m")

colnames(Ecuador_df) = c("x", "y")

rownames(Ecuador_df) = NULL

head(Ecuador_df)

## Units: [m]
##              x         y
## [1,] 594079.73 9721564.1
## [2,] 594365.82 9721900.8
## [3,] 595334.41 9722494.5
## [4,] 595503.63 9722942.7
## [5,] 595385.53 9724374.5
## [6,] 595721.66 9725385.2

El segundo paso es escribir una función que reciba la matriz y aplique las ecuaciones (3) (4) (5).

shoelace = function(vertices){
   x0 = vertices[, "x"]
   x1 = x0[c(2 : length(x0), 1)]
   
   y0 = vertices[, "y"]
   y1 = y0[c(2 : length(y0), 1)]
   
   area = sum(x0 * y1 - x1 * y0) / 2
   
   message("Area:"); print(set_units(area, "km^2"))
   
   xc = sum((x0 + x1) * (x0 * y1 - x1 * y0)) / area / 6
   yc = sum((y0 + y1) * (x0 * y1 - x1 * y0)) / area / 6
   
   message("Centroid:"); c(East = xc, North = yc)
}

El último paso es ejecutar sholace(Ecuador_df); este es el resultado:

## Area:

## 246039.89 [km^2]

## Centroid:

## Units: [m]
##       East      North
##  793562.37 9841009.54

¡Hemos hallado los resultados correctos! Aquí termina la revisión de la shoelace formula, con una última observación: es cierto que la fórmula se ejecuta en un solo paso, pero estas animaciones⁴ progresivas se ven muy bien.